Загадка, задача, шарада, ребус..
- Ответы 9,9 тыс.
- Просмотры 539,1 тыс.
- Создано
- Последний ответ
Лучшие авторы в этой теме
-
G.K. 1 105 постов
-
Wild Red Fox 376 постов
-
Nevernaya 308 постов
-
asc 272 постов
Популярные дни
Самые популярные посты
-
для разминки: загадка на обратный перевод взял я припев некой песни и промтом перевел на английский-немецкий-французский-испанский-русский получилось: . восстановите оригинал))) ответом будет наз
-
@oven666, эта задача не имеет pешения, являясь паpадоксом. Логическая ошибка возникнет и в случае, если циpюльник бpеется сам, и в случае, когда его бpеет кто-то дpугой.
-
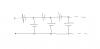
Прочность цепи определяется прочностью слабого звена Емкость батареи не может превышать емкость её конденсатора ответ С
Рекомендуемые ответы
Последние посетители 0
- Ни одного зарегистрированного пользователя не просматривает данную страницу.








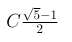
Тут загадывают и разгадывают загадки
"Игрокам следует дождаться поста автора загадки с подтверждением, что загадка отгадана и кому теперь принадлежит ход.
Если отгадавший загадку отказывается задать свою, ход переходит тому, кого он укажет или, при отсуствии оного, к тому, кто первый будет в топе и загадает свою...
Если будут заданы две загадки автор загадки, которая была позже заданной, ОБЯЗАН (!) стереть свою. В противном случае все последующие мессаджи будут являться флудом и подлежат уничтожению."
(с) Хентайщик
Приветствуются:
- авторские загадки, то есть придуманные Вами.
Не приветствуются:
- загадки исключительно "на базу нетривиальных знаний" (вроде "Назовите год рождения Эмми Нетер"), а также "прикольные" загадки - они попахивают идиотизмом.
- классические загадки. Задачу Эйнштейна тут уже несколько раз решали. Да, и на загадку сфинкса ответ известен.
Отредактировано от Nox (см. историю изменений)
Да я жую траву™
[Бессонница]